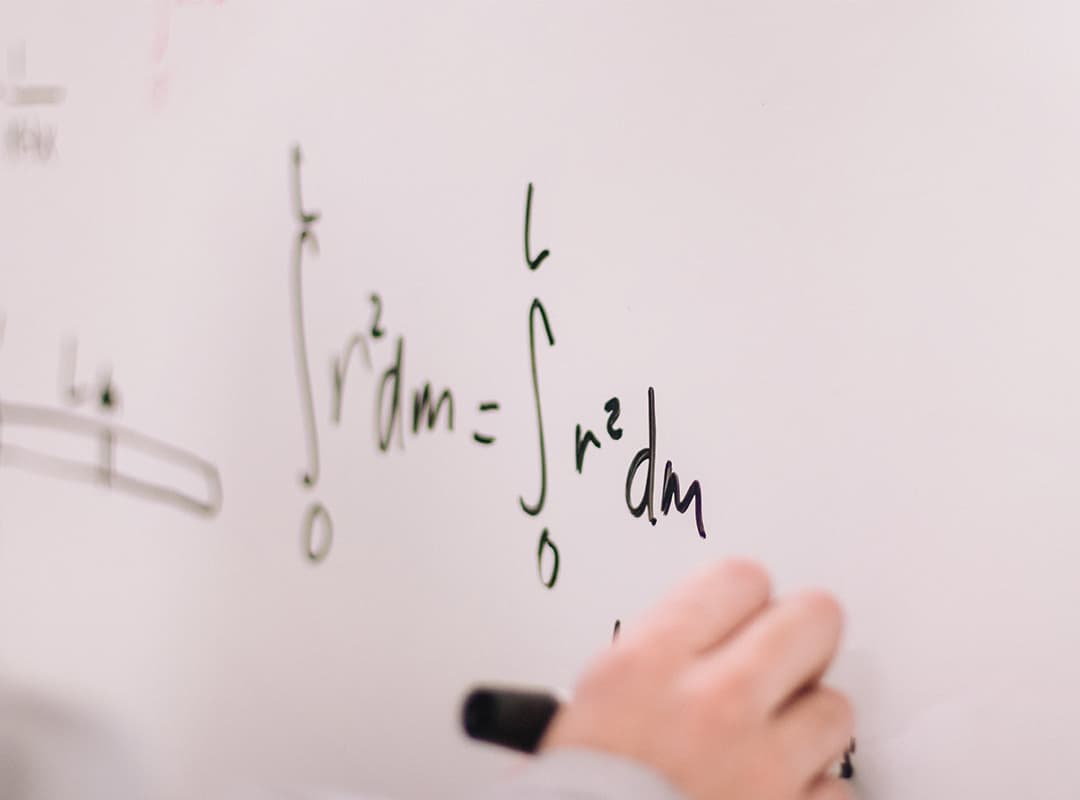The products of theoretical physics are physical theories. Since theoretical physics works precisely with mathematical models, the mathematical consistency of the completed physical theory is an extremely important requirement. The second obligatory property distinguishing theoretical physics from mathematics is the possibility to obtain within the theory predictions for the behavior of Nature under certain conditions (i.e. predictions for experiments) and, in those cases where the result of the experiment is already known, to give agreement with the experiment.
The above allows us to outline the general structure of a physical theory.
It should contain:
- A description of the range of phenomena for which the mathematical model is constructed,
- axioms defining the mathematical model,
- axioms comparing (at least some) mathematical objects with observable physical objects,
- the immediate consequences of the mathematical axioms and their equivalents in the real world, which are interpreted as predictions of the theory.
From this it becomes clear that statements such as “what if the theory of relativity is wrong?” are meaningless. The theory of relativity, as a physical theory that satisfies the necessary requirements, is already correct. If it turns out that it does not converge with the experiment in some predictions, then it means that it is not applicable to reality in these phenomena. It will be necessary to search for a new theory, and it may happen that the theory of relativity will be some limiting case of this new theory. From the point of view of the theory, there is no catastrophe in this. Moreover, it is now suspected that under certain conditions (at energy densities on the order of the Planckian) none of the existing physical theories will be adequate.
In principle, it is possible that for the same range of phenomena there are several different physical theories leading to similar or coinciding predictions. The history of science shows that such a situation is usually temporary: sooner or later either one theory turns out to be more adequate than the other, or it is shown that these theories are equivalent.